气动马达叶轮受力分析

　　气动马达叶轮内气体的流动情况, 可引入以下基本假设:

　　(1)叶轮的叶片数为无穷多,叶片无限薄,因此叶轮内的流动可以看作是轴对称的,并且相对速度的方向与叶片表面相切;

　　( 2)相对流动是定常的;

　　(3)轴向速度在过流断面上均匀分布。为研究叶片与气体交换的能量,需要研究叶片进出口处的气体流动情况,分析叶轮进出口的速度三角形。图3为气流冲击叶轮叶片的作用示意图。

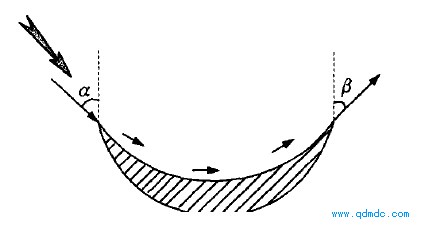
　　图3　气流冲击叶轮叶片示意图

　　由于叶轮是旋转的, 故流体质点相对于静坐标系的绝对运动与相对于叶轮的运动是不同的。

　　根据速度的合成定律, 绝对运动是相对运动和牵连运动的矢量和　c =w + u (5)式中: c为绝对运动速度; w 为流体质点相对于叶轮的速度,称相对速度; u为叶轮上与所考查的流体质点重合点的速度。

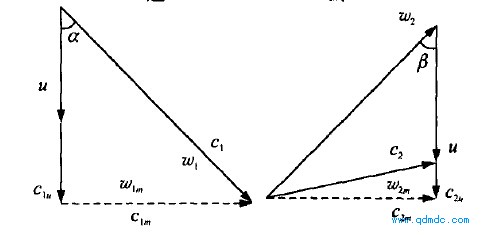
　　由上述分析不难得出叶轮进出口速度的三角形表示,其中, c和w 两个矢量都可以分解为圆周分量和轴向分量,下标m 表示轴向分量,下标u表示圆周分量,叶轮进出口速度三角形如图4所示。

　　设叶轮的转速为n, 常温常压状态下声速为340 m / s,可以得出叶轮输出的转矩M 和机械功率N 分别为　M = qm r( c1u - c2u ) (6)　N =M ×2πn (7)式中: c1u和c2u分别为c1 和c2 的周向分速度,根据速度三角形关系可以得出　c1u = c1 ×cosα (8)　c2u = u2 - w2 cosβ (9)式中: u1 = u2 = u = 2πnr, u为周向叶轮速度;

　　w1 =w2 = u21 + c21 - 2c1 u1 cosα,将式( 8)和式( 9)代入式(6)可得

　　M = qm · ( c1 cosα - u +u2 + c21 - 2c1 ucosαcosβ) (10)式中　c1 =7. 567p0φ(σ) 293 / T0 ×10- 3 0. 258 <σ < =1340 0 <σ < =0. 528