叶片式气动马达转动速度仿真

　我们可以利用 Matlab 的 Simulink 模块可以建立气动马达的仿真模型图,如图 5.1 所示，

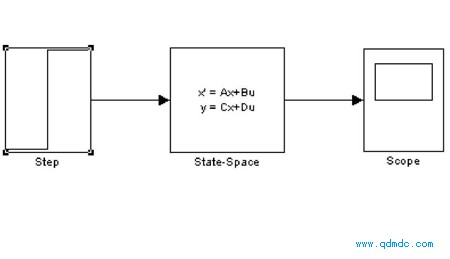
　　图 5.1 气动马达仿真模型图

　　可见气动马达的仿真模型图由三大模块组成:输入阶跃信号模块,状态空间矩阵模块和显示器模块"在气动马达的运动模型中,输入信号

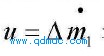
表示的是进气腔室的质量流量增量"此运动模型表达的是进入气动马达腔室的气体质量流量有一增量

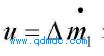
时,马达输出轴转动速度的响应特性"因此可将输入信号看作一个阶跃信号 .

　　由式(4.10)可求出在各工况下进入马达腔室的最大进气质量流量,并取其平均值作为输入信号,经计算在各工况下的进气质量流量平均值如表 5.2 所示:

　　表 5.2 各工况下的马达腔室进气质量流量平均值表

　　因此可将腔室进气质量流量平均值看作阶跃信号输入阶跃信号模块 Step,同时将每一工况下得到的状态空间矩阵 A、B 、C 、D分别输入状态空间模块 State-Space对应的矩阵中,这样就可得到各工况下马达的转速与时间的关系图。为了便于分析气动马达的运行稳定性,我们将气动马达的工况分为五种情况来讨论,它们分别是:气源压力(表压)为 0. 3MPa、0 . 4MPa、0 . 5MPa、0 . 6MPa和 0. 7MPa利用运动模型(5.1)、(5.2)、(5.3)、(5.4)和(5.5)及仿真模型图 5.1 就可以得到在上述五种工况下,气动马达的转速-时间关系图,如图 5.2)图 5.6 所示。根据转速-时间关系图就可以很方便地求出在各个工况下的速度响应动态特性指标参数。本研究考查的动态特性指标参数主要有:

　　1)上升时间 t r:响应曲线从 0 上升到稳态值所需要的时间;

　　2)峰值时间

:响应曲线从 0 到达第一峰值所需要的时间;

　　3)最大超调量 M p:响应偏离稳态值的最大值;

　　4)调整时间 ts :响应到达且维持在稳态值的某个误差百分比范围内所需的时间 ;

　　5)振荡次数

:响应曲线趋于稳定共振荡的周期。

　　为了更直观地分析比较,将每一工况下仿真得到的马达转速-时间关系图分别用图a和图b 表示，其中图a为仿真时间 t = 10s得到的速度-时间关系图,图b 为图a的局部放大图。

　　5.2.1 Ps = 0.3MPa(绝对压力)的转速-时间关系图及其动态特性参数

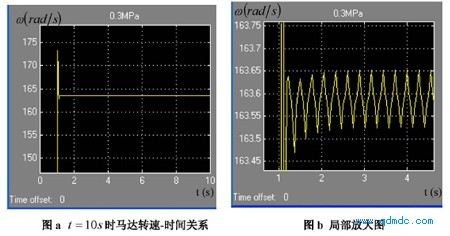
　　图 5.2 气源压力 Ps = 0.3MPa(绝对压力)的转速-时间关系图

　　图 5.2 为气源压力 Ps = 0.3MPa(绝对压力)的转速-时间关系图,此工况下的速度响应曲线的动态特性参数计算如下:

　　1) t r= 1. 0448-1=0.0448( s)

　　2) t p= 1. 0638-1=0.0638(s )

　　3) M p= 173. 3-163.59=9.71(r ad /s)

　　4) t s= 2. 746-1=1.746( s)

　　5) N= ts 2tp=1.7462@ 0.0638=13.683

　　5.2.2 Ps = 0.4MPa(绝对压力)的转速-时间关系图及其动态特性参数

　　图 5.3 气源压力 Ps = 0.4MPa(绝对压力)的转速-时间关系图

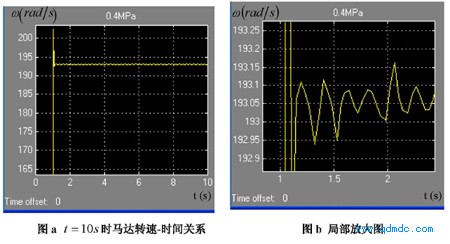
　　图 5.3 为气源压力 Ps = 0.4MPa(绝对压力)的转速-时间关系图,此工况下的速度响应曲线的动态特性参数计算如下:

　　1) t r= 1. 0418-1=0.0418( s)

　　2) t p= 1. 0559-1=0.0559(s )

　　3) M p= 202. 464-193.08=9.384(r ads)

　　4) t s= 1. 98-1=0.98(s )

　　5) N = t s 2tp=0.982@ 0.0559=8.766

　　5.2.3 Ps = 0.5MPa(绝对压力)的转速-时间关系图及其动态特性参数

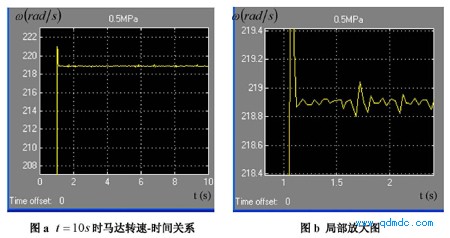
　　图 5.4 为气源压力 Ps = 0.5MPa(绝对压力)的转速-时间关系图,此工况下的速度响应曲线的动态特性参数计算如下:

　　1) t r= 1. 05365-1=0.05365( s)

　　2) t p= 1. 0596-1=0.0596(s )

　　3) M p= 221. 028-218.9=2.128(r ads)

　　4) t s= 1. 27-1=0.27

　　5) N = t s 2tp=0.272@ 0.0596=2.265(s )

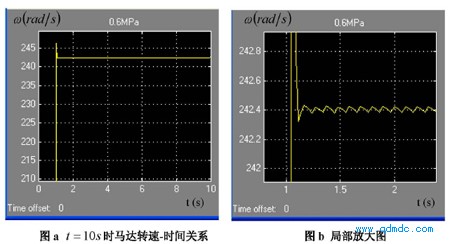
　　图 5.4 气源压力 Ps = 0.5MPa(绝对压力)的转速-时间关系图

　　5.2.4 Ps = 0.6MPa(绝对压力)的转速-时间关系图及其动态特性参数

　　图 5.5 为气源压力 Ps = 0.6MPa(绝对压力)的转速-时间关系图,此工况下的速度响应曲线的动态特性参数计算如下:

　　1) t r= 1. 0444-1=0.0444(s )

　　2) t p= 1. 0557-1=0.0557(s )

　　3) M p= 246. 15-242.405=3.745(r ads)

　　4) t s= 1. 235?1=0.235(s )

　　5) N = t s 2tp=0.2352@ 0.557=2.1095

　　图 5.5 气源压力 Ps = 0.6MPa(绝对压力)的转速-时间关系图

　　5.2.5 Ps = 0.7MPa(绝对压力)的转速-时间关系图及其动态特性参数

　　图 a t = 10s时马达转速-时间关系 图 b 局部放大图

　　图 5.6 气源压力 Ps = 0.7MPa(绝对压力)的转速-时间关系图

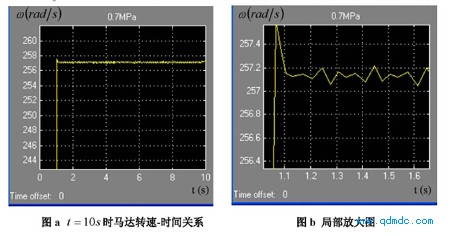
　　图 5.6 为气源压力 Ps = 0.7MPa(绝对压力)的转速-时间关系图,此工况下的速

　　度响应曲线的动态特性参数计算如下:

　　1) t r= 1. 062-1=0.062(s )

　　2) t p= 1. 065-1=0.065(s )

　　3) M p= 257. 6-257.13=0.47(r ads)

　　4) t s= 1. 2783-1=0.2783(s )

　　5) N = t s 2tp=0.27832@ 0.065=2.14